EJERCICIOS.
Inecuación lineal e inecuación con dos variables:
Inecuaciones de segundo grado.
a)
Solución:
Primero calculamos los valores para los que se cumple la igualdad. Para ello, cambiamos la desigualdad por una igualdad. De este modo tendremos una ecuación de segundo grado cuyas raíces determinan los extremos de los intervalos de las soluciones de la inecuación:
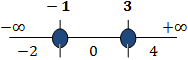
Situamos las raíces en la recta real y obtenemos 3 intervalos:
Escogemos un número al azar de cada intervalo (por ejemplo, x=−2, x=0 y x=4) y comprobamos si para alguno de estos valores se cumple la inecuación. No importa cuál escogemos puesto que el signo de la inecuación se mantiene constante en cada intervalo.
Comprobamos:
Por tanto, la inecuación se verifica en dos de los intervalos:
donde los corchetes indican que los extremos de los intervalos están incluidos (es en ellos donde se da la igualdad de la inecuación).
b)
Solución:
Primero calculamos los valores para los que se cumple la igualdad cambiando la desigualdad por una igualdad y resolviendo la ecuación de segundo grado:
La discriminante de la ecuación es:
Al ser negativo, no existen soluciones reales. Esto significa que se trata de una parábola sin cortes en el eje de las abscisas (eje OX). En otras palabras, la parábola siempre es positiva o siempre es negativa.
Como el término principal es positivo (+6), el vértice está en la parte inferior y, por tanto, la parábola es positiva. Podemos hacer la comprobación dando un valor a x, por ejemplo, x=0:
Por tanto,
Usando la inecuación inicial,
Por tanto, la solución es todos los reales:
Inecuación Racional.
a)
Solución:
Tenemos una fracción y queremos estudiar su signo. Como estamos dividiendo, el signo de la fracción depende de los signos del numerador y del denominador.
Cuando el numerador y el denominador tienen el mismo signo, la fracción es positiva. Si lo tienen distinto, es negativa. Tenemos que ver las distintas posibilidades. Primero analizamos los signos del numerador y del denominador por separado.
Numerador:
Denominador:
La segunda desigualdad es estricta (sin el igual) ya que el denominador no puede ser 0.
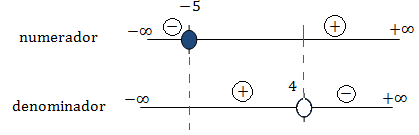
Representamos los valores en dos rectas indicando el signo en cada intervalo:
Hemos representado una recta encima de otra porque ahora tenemos que trabajar con ambas.
El único intervalo para el que el numerador y el denominador tienen el mismo signo (y por tanto, la solución de la inecuación) es:
Siendo ambos positivos en el intervalo. El corchete indica que se incluye el extremo del intervalo ya que en el es donde se cumple la igualdad de la inecuación.
b)
Para que la fracción sea negativa (o cero), el signo del numerador y del denominador han de ser distintos (o el numerador 0).
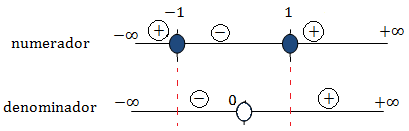
Numerador: es una ecuación de segundo grado, pero por la forma en la que está escrita (factorizada) sabemos que las raíces son 1 y -1. Estudiamos el signo en los tres intervalos:
No olvidemos que x no puede valer 0 en el denominador (denominador nulo).
Mirando las rectas obtenemos los intervalos donde los signos son distintos:
Donde los corchetes indican que los extremos del intervalo están incluidos.


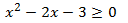
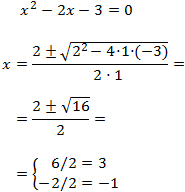

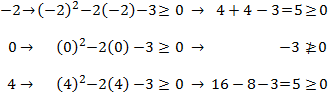
![x pertenece a la unión de los intervalos (-infinito, -1] y [3, + infinito) Resolución de inecuaciones lineales, de segundo grado y racionales: inecuaciones simples, con fracciones (donde usaremos el mínimo común múltiplo), con paréntesis y con paréntesis anidados (unos dentro de otros). Bachiller. Bachillerato.](https://www.matesfacil.com/ESO/inecuaciones/inecuacionB1-4.png)
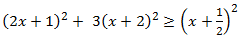
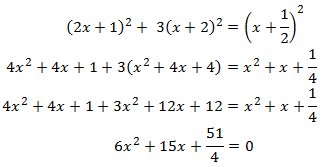
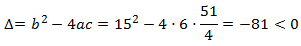
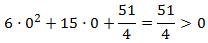
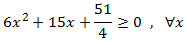
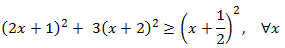
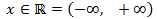
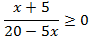
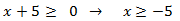
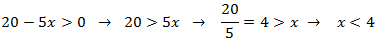
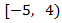
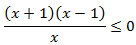
![unión de los intervalos (-infinito, -1] y (0,1] Resolución de inecuaciones lineales, de segundo grado y racionales: inecuaciones simples, con fracciones (donde usaremos el mínimo común múltiplo), con paréntesis y con paréntesis anidados (unos dentro de otros). Bachiller. Bachillerato.](https://www.matesfacil.com/ESO/inecuaciones/inecuacionC3-2.png)






